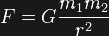Gravity - The Love Story I: Black Holes Are Not 'Universal' Drains

This semester I am teaching a conceptual physics class at LSU that uses minimal mathematics to understand how the Universe works.  Yesterday, we covered the chapter on gravity and my closing question to my students was, "What would happen to the Earth's orbit if the Sun were to become a black hole instantly?"  Assume that it simply changes in size from what it is now to how big a black hole with the same mass would be and the center of mass never changes.

I'm not going to make you wait...  Nothing would happen to the Earth's orbit!

This is one of the most dramatic examples of simply using an equation to tell a story that I have come across.  I suspect that much of the drama comes from the misconception that black holes WILL consume EVERYTHING, turning most people's mental picture of a black hole into a universal drain.

(I know the following analogy is a bit corny, but it makes the point that equations can tell stories and aren't just recipes to combine numbers into new numbers...)


EQUATIONS TELL A STORY

In order to resolve this misconception, consider Newton's law of universal gravitation:

  

Now, don't worry overly that this is an equation because we will be making no calculations.  Instead, we are going to use it as a script for a play.  This play just so happens to be a love story...  ♥


THE CAST OF CHARACTERS

On the left side of "=" we don't have a character, but the ending of our story: F.  (This is the gravitational force that will be felt between two masses.)  We can also think of F as the attraction between our characters.  Therefore, the larger the attraction F, the better the 'Happily ever after...' ending.

The story is told by our characters on the right side of "=": G, m₁, m₂, and r:

• G is a VERY small constant that is fundamental to the Universe.  That is, there is no way to derive its value from any theory, we simply determined this value from measurements.  Since G doesn't change, it is more of a background prop than a character; we don't need to worry about it since the moral of our story will be the same with or without it.
• Next we have our two lovers: masses m₁ and m₂.  I call them lovers because they are attracted to each other (literally since gravity tends to pull mass together).  
• Finally, we have our villain, r, who keeps our lovers apart.  (This is the distance between each of our lovers' center of mass.)  

That is the complete cast of characters in this story!  There are no extras milling around in the background.


THE PLOT

When you multiply G, m₁, and m₂ together and then divide by r² (which is equivalent to r*r), you are able to determine the ending to our story which is the attraction (F) between our lovers.  Now we are able to establish some plot points:

• The more massive either of our lovers (m₁ or m₂) are, the more they will be attracted to each other.
• The farther apart (r) they are, the less they will be attracted to each other; the bigger the number you divide by, the smaller your result.  (The square on r only serves to make the reduction in attraction between our lovers less even faster.  For example, if you double the distance between the lovers, you quarter their attraction.)

THE SUBPLOT

Now let's take a look at some of the more subtle plot points, specifically the properties that determine the attraction of our lovers (m₁ and m₂):

• No unrequited love:  m₁ and m₂ are always equally attracted to each other.  It doesn't matter if one is more massive than the other.  
• Love is blind:  There is nothing in our script which describes the size or shape of our lovers.  Assuming m₁ and m₂ stay the same distance apart and their masses don't change, they will always be equally attracted to each other.  m₁ will love m₂ the same regardless of whether its mass is made up of dense muscle or voluminous blubber. 

"ACTION!"

Now that we have the script to our play, let's see how the ending turns out when we cast the Sun as m₁ and the Earth as m₂.  The scene opens the with Earth orbiting the Sun a fixed distance r away (this is called an astronomical unit, AU, and it is about 93 million miles).  We sit and watch the Sun and the Earth be attracted to each other, but the villain of distance keeps them apart.  In an attempt to overcome our villain, the Sun decides to implode on itself, sucking all of its mass into a ball less than about 3.72 miles across.  Now it is a black hole but, according to our script, the Earth felt no change since its love it blind!  The mass of the Sun didn't change and its center is still in the same place.  Drat, the Sun didn't succeed in increasing its attraction with the Earth!

~ FIN ~

♥  Stay tuned for the next installment of "Gravity - The Love Story"!  We will find out what properties our lovers need to have to come together (that is, what properties a mass needs to have to actually get "eaten" by a black hole).  ♥

Q: If Light is Stretched/Compressed by a GW, Why Use Light Inside LIGO?

Wow!  It's been a while since I've posted...  After the start of a new semester (I have 150 students in the class I am teaching at LSU) and Hurricane Isaac (which shut LIGO Livingston down for almost a week, LSU for 3 days, and left me without power for a while), I am just getting my life back to a somewhat normal routine.  I love even the hectic parts of my life, but I've missed writing about gravitational waves here on Living LIGO!


Q: IF LIGHT IS STRETCHED/COMPRESSED BY A GRAVITATIONAL WAVE, WHY USE LIGHT INSIDE LIGO?

Today I am addressing a question that many professional physicists fully don't understand!  I wrote a little while ago about how light and gravitational waves will stretch out as the Universe expands (this is called redshift).  If an object is coming towards us, its light is compressed (and this is called blueshift).  Basically, if objects are moving, light and gravitational waves will experience a Doppler effect.  I have also written about how a passing gravitational wave will stretch and compress space in perpendicular directions.  When you put these two facts together, you come to the conclusion that the light inside the arms of LIGO is also be stretched and compressed by a gravitational wave.  So, how can we use this light to measure gravitational waves when the light itself is affected by the gravitational wave?

Like I suggested earlier, this is not obvious upon first inspection.  The apparent paradox arises from thinking of laser light as a ruler.  When you think of light, you usually think of it as a wave (which it is, but light is also a particle - however that isn't relevant to this discussion).  Waves have a wavelength -- the distance between each successive wave:

Illustration of wavelength (represented by λ) measured from various parts of a wave. [Source: Wikipedia]

A passing gravitational wave will expand and compress space-time and the wavelength of the light we are using to measure gravitational waves is itself affected by the gravitational wave.  Since LIGO and detectors like it effectively measure the length of its arms and compares them to each other,  how can we rely on light to measure any length changes from a passing gravitational wave?

The solution begins to become clear when you start thinking of the laser light as a clock instead of a ruler.  When the light comes out of the laser, there is a fixed time between each crest of the wave (this is called the period of the wave).  Let's label each crest as 'tick' (like a clock).  Our laser (labeled 'Laser' in the image below) is very stable in that it produces a very consistent wavelength of 1064 nm (near-infrared light).  Because the speed of light is constant no matter how you measure it, that means that there are almost 282 trillion (2.817 x 10¹⁴) 'ticks' every second.  This light is then split into two equal parts (at the 'Beam Splitter' in the image below), one for each arm.

Basic diagram of the LIGO detectors.

Since different things can happen to the light once it is in the arms, let's reference the beam splitter for making length measurements (i.e., let the beam splitter stay in the same place while the gravitational wave alternates squishing and stretching the arms).  A real gravitational wave will cause one arm to shorten and the other to lengthen.  This will also cause the laser wavelength in the shortened arm to decrease (blueshift) and the wavelength in the lengthened arm to increase (redshift).  But there is nothing in the detector that measures wavelength.  What it really measures is the shift in the arrival time of each 'tick' of the wavelength crests.  If the arms stay the same length (no gravitational wave), then the 'ticks' of the laser light come back to the beam splitter at the same time and produces destructive interference where we measure the light (labeled 'Photodetector' in the image above).  If a gravitational wave causes the length of the arms to change and shifts where the 'ticks' of the laser light occur, the two light beams will no longer return to the beam splitter at the same time.  It is this "out of sync" arrival time of the crests of the laser light that produces the interference patter we utilize to detect gravitational waves - we couldn't care less about the actual wavelength of the light (other than it was consistent going into the detector).


READ MORE FROM OTHER LIGO SCIENTISTS:

A wonderful, concise summary on why light can be used in gravitational wave detectors like LIGO has been published in American Scientist here.  The author, Peter Shawhan, is an associate professor at the University of Maryland, College Park.

There is also an article in the American Journal of Physics (vol. 65, issue 6, pp. 501-505) titled "If light waves are stretched by gravitational waves, how can we use light as a ruler to detect gravitational waves?"  This is a more technical article by Peter Saulson who is a professor at Syracuse University.