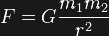Happy New Year!

I can't believe how long it's been since I've last blogged - I've had so many ideas of stories to post, but I've also had some life issues that have kept me away.  Not to worry!  My most important resolution for 2013 is to write blog posts a few weeks ahead of time so that I can still post weekly even when life gets in the way.  I will be back in full force in 2013!  Expect posts on Thursdays, unless there is something timely I want to share before then.  I will make sure to post on Twitter when I a new post is available so if you don't follow me already, please follow @livingligo.

This is a smiley face the deicing crew at the Pittsburgh International Airport made in the snow.  As seen through the deicing fluid on the window of my plane on the evening of 29 December 2012.

2012

This year has been a year of many changes for me.  My days as a postdoc have come to an end and I now hold a dual position with Caltech as a scientist at the LIGO Livingston Observatory and as a physics instructor at LSU.  It is great being back in the classroom but that is also something that has kept me from posting as much as I would like.  It takes a lot of time to create interesting lectures for a class of 150 students and handle all of the class administration myself (office hours, grading, etc.).  This semester I am teaching the second semester of physical science (astronomy, chemistry, earth science) and will only have a 30 students.  I am very excited about the more personal instruction I will be able to do!

There have also been many changes at LIGO.  When I first started working at the Livingston observatory in 2007, there were about 25-30 people who worked there on a daily basis.  Starting with the Advanced LIGO preparations in 2010, we nearly doubled the number of daily staff.  Since the installation is well underway, we no longer need to have so many people on site (having too many people on site while we are looking for gravitational waves will cause ground vibrations that will decrease our sensitivity).  The parking lots are noticeably less full and it is starting to feel a little lonely even though we still have more people working on site than when I started.

As far as my personal life is concerned, I'm glad that 2012 is over.  It has been full of drama and uncertainty and it is one of the things that have been getting in the way of keeping up with this blog and my career in general.  But I wouldn't change a moment of it since I have so many great people around me, at home and at work, who care for me. 


2013

This coming year will prove to be exciting!  The installation of Advanced LIGO should be completed and the first commissioning (use of the detector to fine tune it to its best sensitivity) started.  This is always an interesting time when you get to use the detector for the first time and solve novel problems.  I will be sure to tell you all about them here! 

I will also continue teaching at LSU.  As I mentioned above, I will be teaching the second semester of physical science with about 30 students.  I also expect to teach a masters degree class on inquiry learning for in-service teachers this summer (I've done this class twice before with LSU).  

Of course, the most exciting events are usually the unexpected.  I look forward to sharing the professional and personal excitement with you here.

Thank you to all of my readers, followers on Twitter, and those who found me through a search engine!  Keep coming back for more!

What are you looking forward to this year?

Gravity - The Love Story II: Starstruck!

So, where was I when I last posted...  Ahh... The great corny love story between two objects bound together by gravity.  I started that post asking what would happen to the Earth if the Sun were to suddenly become a black hole.  Many people think that the Earth would be sucked in because they assume that a black hole will suck everything into it like water going down a drain.  But, from careful examination of the universal law of gravitation and the story it tells, we see that isn't the case and the Earth will stay in the same orbit that is it now - no closer and no farther away.

But what about an object flying by a black hole (or any other massive object) instead of being in a nice stable orbit (like the Earth is in the previous example)?  This makes things a little more complicated, so I am going to let go of telling a love story.  That being said, there will be more equations here, but like the previous love story post the equations will only serve to help tell the story and we will not be using any numbers.


THE FATE OF A COSMIC WANDERER

Instead of looking at the universal gravitation law, we are going to look at how a passing object comes to be in orbit, or not, around another object (this governed by Kepler's laws of planetary motion).  To keep things simple, let's assume that the moving object has much, much less mass than the object it's passing (this is so that we can ignore the motion of the big object due to its gravitational attraction to the passing object).  Basically, picture something small whizzing through space (I'll call this the small object) that passes by a star or black hole (I'll call this the big object).  It is now safe to assume that any motion caused by gravity is going to be seen in the small object.


IT'S ALL ABOUT THE SPEED

The one factor that completely determines the fate of the small object is its speed.  If this speed is great enough, then the small object will be able to escape the big object, though its speed and direction will have changed.  The minimum speed at which the small object will not be captured into an orbit is called the escape velocity:

Here, we see that the escape velocity, v_e, changes as the square root of 1/distance (1/r) between the objects' centers.  That means that the closer the small object is to the big object, the more speed it must have in order not to get caught by it; the farther away, the less speed it needs to escape.  2GM is a constant value and never changes; G being the universal gravitational constant and M being the mass of our big object.


ORBITS AND ELLIPSES

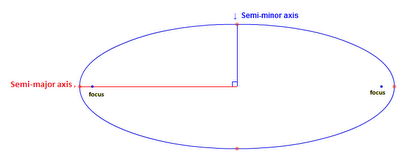
Any speed less than the escape speed and the small object will be captured by the big object and will likely start orbiting the big object (or collide with it, we'll get to that later).  Let's say that we are traveling at a speed less than the escape velocity.  Kepler's laws of planetary motion (which are a consequence of gravitation) provide that the shape of the orbit is an ellipse (an oval shape).  Instead of having one center like a circle does, an ellipse has 2 each called a focus.  A classic way to draw an ellipse for yourself is to put two pins into a piece of paper, put a loop of string around the pins, place a pen in the loop and pull the loop taut.  The shape that you draw doing this is an ellipse:

[Image from: Wikipedia]

Here, each pin is a focus.  This is what having 2 "centers" means - if you were to draw a shape using this same method but using only one pin, then you would draw a circle (the pin being the true center).  When talking about an orbit of a very massive object and much smaller object (like we have in this example, or like the Earth orbiting the Sun), the more massive object will be located at a focus and there isn't anything at the other focus.

The speed of the object determines the shape of orbit:

Here v is the speed of the orbiting object (which is less than the escape velocity), μ is a constant (G times the mass of the big object), r is the distance from the objects' centers when the velocity is measured, and a is the semi-major axis of the ellipse (the distance between the midpoint of the foci and the farthest point of the ellipse). 

[Image from: Wikipedia]

STARSTRUCK!

Under what conditions does the small object collide with the big object?  So far it sounds like the small object is either going to escape the gravitational pull of the big object or start orbiting it.  Can a black hole (assuming it's our big object) ever "swallow" anything?  Yes, indeed, but only under certain conditions...

To determine the conditions for an object to be swallowed by a black hole or collide with a star, we need to realize that neither of these objects is a nice point as we have been treating them (well, the singularity inside the black hole is a nice point, but more on that below).  Instead, objects occupy a volume and the points we were considering were really the center of mass of the object (approximately the actual center for a spherical object).  So, the small object will collide with the big object if the radius of the big object is more than the distance of closest approach of the small object's orbit.  This distance is called periapsis and is the distance along the red line (the semi-major axis) between the ellipse (orbit) and the focus (the big object) in the previous figure.  If a star has a radius of this or more, then the small object will slam into it.

NOTE:  This scenario for collision (and the one for merger with a black hole below) assumes that the objects only interact through gravity.  That means that there is no consideration here for other forces like the interactions of the objects' magnetic fields (if they have them) or resistance from the matter and radiation that stars tend to spew out.


HUNGRY, HUNGRY, BLACK HOLES

But what about the specific case of a black hole?  I mention that there is a point-like singularity in the black hole where all the mass is located.  How do we determine the shape of the whole black hole?  First, consider why a black hole is called "black"; because the gravity inside of it is so strong that the speed of light is less than the escape velocity (now you can think of our small object as a photon of light).  Since nothing can travel faster than the speed of light, nothing can escape a black hole.  So we define the edges of the black hole to be the radius at which the escape velocity equals the speed of light.  This radius is called the event horizon.  Therefore, an object (even a photon) will merge with a black hole when the distance of closest approach of its orbit is equal to or less than the event horizon.

Now that's what I call "starstruck" lovers!  Get it?  The small object strikes the big object which could be a star...  Okay, I know it's lame, but that's why I'm a physicist and not a comedian (though I do try!).

---

 

♥  Speaking of love, happy anniversary to my husband, Derek, who is always nice enough to proofread these posts.  We've been together for 16 years, married for 9 and looking forward to many more!  ♥

Happy Halloween!

Wow!  I can't believe how long it has been since I've posted.  I've been horribly busy keeping up with teaching at LSU (and trying my best to make my lectures interesting), getting my LIGO work done (we are preparing for the 3rd software engineering run for Advanced LIGO [read about the first one here]), and some personal life complications that we all deal with from time to time.  I understand better why the blessing, "May you live in interesting times," is more of a curse.

So, to tide you over until my next full post (tomorrow), here is the feature presentation of the Science Education Center's monthly Science Saturday - Halloween Edition (2011):

Here, William Katzman (Science Education Center Lead) plays a laid back fellow with some paranormal explanations of "spooky phenomena".  I play a scientist who explains all of the phenomena in terms of science.  Before the day of the presentation, we decided what spooky phenomena we were going to use, but we never rehearsed the show - I'm surprised it turned out so well (if I say so myself)!

Gravity - The Love Story I: Black Holes Are Not 'Universal' Drains

This semester I am teaching a conceptual physics class at LSU that uses minimal mathematics to understand how the Universe works.  Yesterday, we covered the chapter on gravity and my closing question to my students was, "What would happen to the Earth's orbit if the Sun were to become a black hole instantly?"  Assume that it simply changes in size from what it is now to how big a black hole with the same mass would be and the center of mass never changes.

I'm not going to make you wait...  Nothing would happen to the Earth's orbit!

This is one of the most dramatic examples of simply using an equation to tell a story that I have come across.  I suspect that much of the drama comes from the misconception that black holes WILL consume EVERYTHING, turning most people's mental picture of a black hole into a universal drain.

(I know the following analogy is a bit corny, but it makes the point that equations can tell stories and aren't just recipes to combine numbers into new numbers...)


EQUATIONS TELL A STORY

In order to resolve this misconception, consider Newton's law of universal gravitation:

  

Now, don't worry overly that this is an equation because we will be making no calculations.  Instead, we are going to use it as a script for a play.  This play just so happens to be a love story...  ♥


THE CAST OF CHARACTERS

On the left side of "=" we don't have a character, but the ending of our story: F.  (This is the gravitational force that will be felt between two masses.)  We can also think of F as the attraction between our characters.  Therefore, the larger the attraction F, the better the 'Happily ever after...' ending.

The story is told by our characters on the right side of "=": G, m₁, m₂, and r:

• G is a VERY small constant that is fundamental to the Universe.  That is, there is no way to derive its value from any theory, we simply determined this value from measurements.  Since G doesn't change, it is more of a background prop than a character; we don't need to worry about it since the moral of our story will be the same with or without it.
• Next we have our two lovers: masses m₁ and m₂.  I call them lovers because they are attracted to each other (literally since gravity tends to pull mass together).  
• Finally, we have our villain, r, who keeps our lovers apart.  (This is the distance between each of our lovers' center of mass.)  

That is the complete cast of characters in this story!  There are no extras milling around in the background.


THE PLOT

When you multiply G, m₁, and m₂ together and then divide by r² (which is equivalent to r*r), you are able to determine the ending to our story which is the attraction (F) between our lovers.  Now we are able to establish some plot points:

• The more massive either of our lovers (m₁ or m₂) are, the more they will be attracted to each other.
• The farther apart (r) they are, the less they will be attracted to each other; the bigger the number you divide by, the smaller your result.  (The square on r only serves to make the reduction in attraction between our lovers less even faster.  For example, if you double the distance between the lovers, you quarter their attraction.)

THE SUBPLOT

Now let's take a look at some of the more subtle plot points, specifically the properties that determine the attraction of our lovers (m₁ and m₂):

• No unrequited love:  m₁ and m₂ are always equally attracted to each other.  It doesn't matter if one is more massive than the other.  
• Love is blind:  There is nothing in our script which describes the size or shape of our lovers.  Assuming m₁ and m₂ stay the same distance apart and their masses don't change, they will always be equally attracted to each other.  m₁ will love m₂ the same regardless of whether its mass is made up of dense muscle or voluminous blubber. 

"ACTION!"

Now that we have the script to our play, let's see how the ending turns out when we cast the Sun as m₁ and the Earth as m₂.  The scene opens the with Earth orbiting the Sun a fixed distance r away (this is called an astronomical unit, AU, and it is about 93 million miles).  We sit and watch the Sun and the Earth be attracted to each other, but the villain of distance keeps them apart.  In an attempt to overcome our villain, the Sun decides to implode on itself, sucking all of its mass into a ball less than about 3.72 miles across.  Now it is a black hole but, according to our script, the Earth felt no change since its love it blind!  The mass of the Sun didn't change and its center is still in the same place.  Drat, the Sun didn't succeed in increasing its attraction with the Earth!

~ FIN ~

♥  Stay tuned for the next installment of "Gravity - The Love Story"!  We will find out what properties our lovers need to have to come together (that is, what properties a mass needs to have to actually get "eaten" by a black hole).  ♥

Q: If Light is Stretched/Compressed by a GW, Why Use Light Inside LIGO?

Wow!  It's been a while since I've posted...  After the start of a new semester (I have 150 students in the class I am teaching at LSU) and Hurricane Isaac (which shut LIGO Livingston down for almost a week, LSU for 3 days, and left me without power for a while), I am just getting my life back to a somewhat normal routine.  I love even the hectic parts of my life, but I've missed writing about gravitational waves here on Living LIGO!


Q: IF LIGHT IS STRETCHED/COMPRESSED BY A GRAVITATIONAL WAVE, WHY USE LIGHT INSIDE LIGO?

Today I am addressing a question that many professional physicists fully don't understand!  I wrote a little while ago about how light and gravitational waves will stretch out as the Universe expands (this is called redshift).  If an object is coming towards us, its light is compressed (and this is called blueshift).  Basically, if objects are moving, light and gravitational waves will experience a Doppler effect.  I have also written about how a passing gravitational wave will stretch and compress space in perpendicular directions.  When you put these two facts together, you come to the conclusion that the light inside the arms of LIGO is also be stretched and compressed by a gravitational wave.  So, how can we use this light to measure gravitational waves when the light itself is affected by the gravitational wave?

Like I suggested earlier, this is not obvious upon first inspection.  The apparent paradox arises from thinking of laser light as a ruler.  When you think of light, you usually think of it as a wave (which it is, but light is also a particle - however that isn't relevant to this discussion).  Waves have a wavelength -- the distance between each successive wave:

Illustration of wavelength (represented by λ) measured from various parts of a wave. [Source: Wikipedia]

A passing gravitational wave will expand and compress space-time and the wavelength of the light we are using to measure gravitational waves is itself affected by the gravitational wave.  Since LIGO and detectors like it effectively measure the length of its arms and compares them to each other,  how can we rely on light to measure any length changes from a passing gravitational wave?

The solution begins to become clear when you start thinking of the laser light as a clock instead of a ruler.  When the light comes out of the laser, there is a fixed time between each crest of the wave (this is called the period of the wave).  Let's label each crest as 'tick' (like a clock).  Our laser (labeled 'Laser' in the image below) is very stable in that it produces a very consistent wavelength of 1064 nm (near-infrared light).  Because the speed of light is constant no matter how you measure it, that means that there are almost 282 trillion (2.817 x 10¹⁴) 'ticks' every second.  This light is then split into two equal parts (at the 'Beam Splitter' in the image below), one for each arm.

Basic diagram of the LIGO detectors.

Since different things can happen to the light once it is in the arms, let's reference the beam splitter for making length measurements (i.e., let the beam splitter stay in the same place while the gravitational wave alternates squishing and stretching the arms).  A real gravitational wave will cause one arm to shorten and the other to lengthen.  This will also cause the laser wavelength in the shortened arm to decrease (blueshift) and the wavelength in the lengthened arm to increase (redshift).  But there is nothing in the detector that measures wavelength.  What it really measures is the shift in the arrival time of each 'tick' of the wavelength crests.  If the arms stay the same length (no gravitational wave), then the 'ticks' of the laser light come back to the beam splitter at the same time and produces destructive interference where we measure the light (labeled 'Photodetector' in the image above).  If a gravitational wave causes the length of the arms to change and shifts where the 'ticks' of the laser light occur, the two light beams will no longer return to the beam splitter at the same time.  It is this "out of sync" arrival time of the crests of the laser light that produces the interference patter we utilize to detect gravitational waves - we couldn't care less about the actual wavelength of the light (other than it was consistent going into the detector).


READ MORE FROM OTHER LIGO SCIENTISTS:

A wonderful, concise summary on why light can be used in gravitational wave detectors like LIGO has been published in American Scientist here.  The author, Peter Shawhan, is an associate professor at the University of Maryland, College Park.

There is also an article in the American Journal of Physics (vol. 65, issue 6, pp. 501-505) titled "If light waves are stretched by gravitational waves, how can we use light as a ruler to detect gravitational waves?"  This is a more technical article by Peter Saulson who is a professor at Syracuse University.

My New Jobs and Working in Academia

THE NEW JOBS

I've talked before about my current position as a postdoc (short for postdoctoral scholar/researcher/fellow/etc.).  This is a temporary position very much like a medical doctor's residency.  I've held this position for the past 5 years and I've loved it, so much so that I managed to land myself a more permanent position, or I should say positions since I now have 2 jobs.

My first job that will be replacing my postdoc (which is up at the end of the month) is "Data Analysis and EPO Scientist" for Caltech but working at the LIGO Livingston Observatory (EPO stands for Education and Public Outreach).  This is a half-time position that will allow me to continue my LIGO research and continue to perform outreach.  Basically, this new scientist job at LIGO will let me to keep doing what I've been doing for the last 5 years.

My second job is an instructor position in the LSU physics department.  This semester I am teaching conceptual physics (PHSC 1001: Physical Science) which is sometimes referred to as "physics for poets".  I am especially excited about teaching the class at LSU because many of the students are future teachers themselves.  I've taught the equivalent course to this while I was at Penn State (PHYS 001: The Science of Physics).  This was the one course I had complete control over while I was at Penn State: including text book selection, lecture & exam creation, etc.  I picked this class because it is hard to teach.  Through my previous teaching experience, I discovered that the less math you use in a physics class, the harder it is to teach.  Calculus-based physics is MUCH easier to teach than algebra-based; not because the students in the calculus-based physics class are smarter (which isn't true), but because a teacher can use math as a crutch and not have to truly articulate concepts.


THE GOOD AND THE BAD

I am really thrilled about my jobs.  Not only do I have a job (with benefits) in this economic climate, but it is in my field and doing what I love to do.  I am also back in the classroom which I missed (but loved the work in outreach I've been doing).  I get to continue doing to LIGO research.

In a sense, I have a very non-traditional "professorship" since I get to teach and do research.  The reason this isn't really a professorship is that I do not have the ability to earn tenure.  In academia, after a certain amount of time (usually 7 years) you are eligible for a promotion that makes you a permanent member of the faculty at the school.  In higher education, the evaluation criteria usually include the quality of your research (usually measured on the amount of grants you obtained and papers that you published), your teaching, and your service to the school and the profession.  At very big research schools, much more weight is placed on research; in smaller liberal arts colleges, teaching is often more important.  The fact that I am in a non-tenure track position is good in that I don't have to worry about obtaining my own research funds or publish stacks of papers and it is bad in that I am never going to have the security that tenure could bring me.  Of course, I have the option of leaving my current positions in the future and finding a tenure-track job (which isn't easy to do these days).

Another good aspect about my split position is that it think it is pretty hard to get laid off from two different jobs at the same time.  I guess that's a kind of job security...  I may not have tenure but it will be hard for me to be completely unemployed.

Ultimately, I am thrilled that two different universities are willing to claim me and I still get to do what I love...  It doesn't get much better than that!

The Journey of a Gravitational Wave III: GWs Stretch Out

What happens to a gravitational wave between when it is produced and when LIGO can detect it?  It turns out not much, which makes it a key new medium in which to observe the Universe!

Today I will be discussing how a gravitational wave can get stretched during its journey to Earth.  Previously, we have discussed how gravitational waves can be bent away from a straight path and how things cannot absorb or reflect a gravitational wave.


THE DOPPLER EFFECT

If you have ever been passed by an ambulance or police car with its sirens on, then you likely noticed that as the sound from the siren approached you, the tone was higher than when the siren passed you.  This is due to something called the Doppler effect.  As the source of a sound is moving toward toward you, the distance between the sound wave's crests (wavelength) are compressed, resulting in a higher frequency.  We hear higher frequencies as higher tones.  Conversely, when the source of a sound is moving away from you, the sounds wave's crests are stretched apart resulting in a lower frequency and a lower tone.  Consider the following animated example:

Animated example of the Doppler effect: how motion and cause the wavelength of sound to be affected.
[Image from Wikipedia]

In the beginning of this animation, the car is not moving and the sound waves have the same wavelength both in front and behind the car.  Once it starts moving forward (to the left), the sound waves in front of the car are closer together and the sound waves behind the car are farther apart.  This results in us hearing a higher tone when you are in front of the car and a lower tone when you are behind the car.


COSMOLOGICAL REDSHIFT

This Doppler effect can also affect the wavelength of light and of a gravitational wave depending on the motion of the object creating the waves.  First, let's think about what happens to light.  As the source moves toward you, the wavelength of the light will get shorter.  Since we can't hear light, instead of hearing a higher tone, we will see the light to be shifted toward the blue end of the spectrum (where the shortest wavelengths we can see are).  This is called blueshift.  For a source moving away from us, the wavelengths would be longer and we would see the light shifted toward the red end of the spectrum (where the longest wavelengths we can see are).  This is called redshift.

We can measure this cosmological Doppler effect by measuring the spectral signatures of stars.  Below is an example of such a spectral signature.  Stars give off almost every color of light, but there are particular colors that get absorbed by different elements before that light can make it to Earth.  Those absorbed colors show up as dark lines in an otherwise complete spectrum of colors:

The optical spectrum from our Sun (left) compared to the optical spectrum of a supercluster of galaxies (right).  Note that there are similar dark lines (from absorption of those wavelengths by different chemical elements), but the lines on the right are shifted toward the red end of the spectrum.  This phenomena is called "redshift" because of this.  [Source: Wikipedia]

The spectrum to the left is what we observe from our local star, the Sun.  The spectrum on the right is from a distant cluster of galaxies (containing many stars).  Note that the spacing of the dark lines is essentially the same, just shifted toward the red end of the spectrum (this is highlighted by the arrows).  That means that this cluster of galaxies is moving away from us.  Just about everything (but not quite) in the Universe shows this redshift which implies that the Universe is expanding!  (There is more than one cause of redshift, but we will only be discussing the redshift due to the expanding Universe in this blog post.)

Redshift is measured by the change in wavelength of light (or a gravitational wave) divided by the wavelength of light if the source wasn't moving.  For the spectrum example here, this would be the amount the color of the light changed (the difference between the right and the left side) divided by its original color (the left side).  The redshift is a result of the Doppler effect; it can also be used to measure an object's velocity.  To do that, we need to determine the proportionality constant between redshift and velocity.  This constant is known as the Hubble constant, H (named after Edwin Hubble who first determined this relationship).  The best estimate of this constant is currently:

H = 71.0 ± 2.5 km/s/Mpc
        67.2 ± 1.2 km/s/Mpc
(revised on 20 March 2013 with the parameters released by Planck)

This means that for every light-year away an object is, its velocity away from us increases by about 257 feet/hour.  (This may not sound like much, but a light-year is really a very small distance in the Universe; our own galaxy is about 110,000 light-years across!)  This expansion is believed to have originated with the Big Bang.  So, will the Universe expand forever?  Will it slow to a stop?  Will it stop expanding and start shrinking until everything is a compact ball again (this is called the Big Crunch)?  From current observations, the ultimate fate of the Universe appears to be an eternal slowing expansion which will cause all of the energy to be evenly distributed throughout this even larger Universe (compared to now).  That means that there won't be enough energy in any one place to make anything happen (all events in the Universe need an imbalance in energy).  This is called the Big Freeze or the heat death of the Universe.  However, more observations (especially of things like dark matter and dark energy) of our Universe are needed before we can be sure of the Universe's future.

BLUESHIFT

There are a few things in our Universe that are moving towards us and therefore have a blueshift.  Of most note is the Andromeda Galaxy which is moving towards us at about 300,000 meters/s (671,801 mph).  This is because our Milky Way Galaxy and the Andromeda Galaxy are gravitationally bound to each other; this means that the gravitational attractions between these two galaxies are greater than the expansion of the Universe.  In the future, our two galaxies will collide, but not for an estimated 4.5 billion years.  This is also about the time the that our Sun will become a red giant and all life on Earth will be extinct by then anyway!  I wouldn't stress about it if I were you :P

Also, portions of rotating galaxies can be blueshifted.  In this case, the side that is rotating toward us will be blueshifted and the part that is rotating away from us will be redshifted.


GRAVITATIONAL WAVES AND REDSHIFT

Just like redshift stretches out the wavelength of light, the expansion of the Universe will also stretch out the wavelength of a gravitational wave during its journey to Earth.  In a previous post, I discussed what gravitational waves would sound like if you put their signal through a speaker (remember: gravitational waves don't make sound!).  So, I decided I wanted to hear what the change in the sound of a gravitational wave is due to different amounts of redshift.  I did the calculations, generated the sounds, and assembled them into the video below for your viewing pleasure:

So, how can we make use of the redshifting of a gravitational wave to learn more about our Universe?  Well, most astronomers and physicists don't believe that the rate of expansion of the Universe (the Hubble constant, H, above) has been the same since the Big Bang.  Particularly, there is a period believed to have existed in the past history of the Universe called inflation which is a time of rapid expansion.  From a certain kind gravitational wave source, we will be able to measure the Hubble constant around the neighborhood of the source.  This will be a direct probe of how the expansion of the Universe (the Hubble constant) has changed through the history of the Universe because observing objects in the distance is the same as observing them as they were in the past (e.g. observing an object 1 light-year away is the same as observing it as it was a year ago since light and gravitational waves travel at the speed of light - at least gravitational waves are expected to travel at the speed of light!).

The Journey of a Gravitational Wave II: GWs Get Bent

What happens to a gravitational wave between when it is produced and when LIGO can detect it?  It turns out not much, which makes it a key new medium in which to observe the Universe!

Last week, I began discussing what happens to a gravitational wave as it makes its way from its source to Earth; specifically that gravitational wave can travel through matter and come out the other side unchanged!  Today's post talks about how the gravitational effects of other masses in the Universe can deflect the gravitational wave from its otherwise straight path.


GRAVITATIONAL LENSING

Let's think again about what happens to light on its way to Earth.  We know from the last post that any matter light comes into contact with will reflect or absorb at least part of the light.  There is also another effect called gravitational lensing that causes light to bend around massive objects due to the massive object's gravitational influence.  This is caused by light following its natural path on curved spacetime (or light being bent by a gravitational field since we've previously established that the curvature of spacetime is a representation of the strength of the gravitational field there).  The first thing that pops into my mind that illustrates something following its natural path on a curved surface is miniature golf:

This is hole 13 at Safari Mini Golf in Vero Beach, FL.  This image is taken from a review of this course and can be read here.

Consider the example hole in the above image.  After you get your ball past the three bumps, there is a wonderful bowl-like curved portion behind the target hole (if you look very closely, you can see the hole directly after the last bump and in the center).  If you hit your ball into this area, the ball's trajectory will change from a straight path to a curved one.  If your ball begins its path on the left side of the bowl, it will curve right; if your ball enters the bowl from the right, it will curve left.  The same thing happens for light and gravitational waves that pass by a massive enough object to cause a significant depression in spacetime (i.e. a strong gravitational field):

The bending of light from a star that is really behind the Sun but appears to be to the side of the Sun.
[Credit: Ethan Siegel of Lewis & Clark College, OR]

The the light from a star, galaxy, or other source travels through the depression in spacetime made by a nearby massive object (in the image above it is the Sun).  The path that light takes is curved just like the golf ball in the miniature golf example above.  But our brains are wired to assume that any light that enters our eyes has come to us in a straight line (which is how light usually travels) so we perceive the location of the source to be directly behind where it appears to be.  Therefore, while the star is really behind the Sun (at point A in the image above), it appears to us to be to the side of the Sun (at point B).  This bending effect is called gravitational lensing and it applies to gravitational waves just like it does to light.


KINDS OF GRAVITATIONAL LENSING

The example of gravitational lensing given above was one of the first observational proofs that Einstein's general relativity was correct.  Before relativity, there was already a prediction of the bending of light due to Newtonian gravity (what we use in our everyday life) but Einstein predicted the bending effect should be twice that predicted without relativity.  In 1919, there was a total eclipse of the Sun which would allow those stars that are near the Sun to become visible.  Images of the eclipse were taken and it was seen that the shift in the position of stars near the Sun was indeed twice that of the shift predicted by Newtonian gravity.

There are also kinds of lensing that produce much more dramatic effects than shifting the position of stars!  Things like large galaxies and clusters of galaxies can cause the light from objects behind them to be split up to form multiple, separate, and complete images. 

[Image from NASA]

The image above shows gravitational lensing of a quasar and a galaxy by a distant galaxy cluster SDSS J1004+4112 (SDSS indicates that it was discovered by the Sloan Digital Sky Survey).  Each image of the quasar is of the same single object; the same is true of the galaxy! 

You may notice that each of the images are a little different from each other.  This is due to the distortion that a gravitational lens can cause.  This effect is illustrated well in the simulation below of a black hole creating a gravitational lens as it passes in front of a galaxy:

[Image from Wikipedia]

Note the circular distortion of the light from the galaxy as the black hole passes by.  When the black hole is directly in front of the galaxy, there is a circular halo of lensed light around it.  This halo called an Einstein Ring can can be caused by any extremely massive object (black hole, galaxy, galaxy cluster, etc.).

[Image credited within the image and retrieved from Wikipedia.]

HOW LENSING AFFECTS THE SEARCH FOR GRAVITATIONAL WAVES

Gravitational lensing affects both light and gravitational waves.  This produces spectacular images of objects using light, but LIGO will not produce images and the sources that produce gravitational waves are more point-like (a black hole, a star exploding, etc.) than large scale objects (like galaxies which are thousands of light-years across).  The effect that will most likely be seen in gravitational waves is their focusing; the bending of gravitational waves can produce more intense gravitational waves from the lensed source (similar to a magnifying glass focusing light to a smaller point).  This paper suggests that the galactic center of the Milky Way could increase the intensity of a source in our galaxy (bur behind the galactic center) up to 4000x.  Also, if a gravitational wave is emitted from a galaxy that has multiple images from lensing, then that gravitational wave will come from each image!

However, most sources will not have appreciable lensing.  While this is something we will always need to consider while conducting gravitational-wave astronomy, it isn't something that is likely to change the information contained on the gravitational wave noticeably (and that's a good thing)!

The Journey of a Gravitational Wave I: GWs Cast No Shadows!

What happens to a gravitational wave between when it is produced and when LIGO can detect it?  It turns out not much, which makes it a key new medium in which to observe the Universe!

In order to make this information more digestible, I will address one aspect of a gravitational wave's journey through space.  Today's topic discusses how the Universe is essentially transparent to a gravitational wave.  Future editions will discuss how matter can bend gravitational waves (gravitational lensing) and how the expanding Universe can stretch out (redshift) gravitational waves.


GRAVITATIONAL WAVES CAST NO SHADOWS:

First, let's think about what happens to light.  As light travels through the Universe, any time that it encounters other matter, some of the light is absorbed by the matter or reflected away from its original path.  The opposite happens for a gravitational wave; it can pass through matter and come out the other side unchanged (although there are some negligible effects)!  That means that there is no such thing as a gravitational-wave shadow and nothing can obscure our detection of a gravitational wave!


The Spacetime Explanation:

But why is this?  In a previous post, I described a gravitational wave as a change in the gravitational field moving out into the Universe.  This change in gravitational field is often illustrated as a ripple, or wave, on spacetime (where the steepness of the curvature of spacetime represents the strength of the gravitational field, or the gravitational force a mass would feel, there).  Let's look at what the Earth sitting on space-time looks like:

This picture isn't a perfect representation since the size of the Earth will affect the shape of the depression and this has no effect on real spacetime.  Also, this is a simplified 2-dimenional representation of 3-dimensional (or a snapshot of the 4-dimensional spacetime) space.  But if you were to imagine giving a corner of this flexible grid (spacetime) a swift shake, the Earth in the middle would be affected by it but it would not impede the wave.  So, this is an example of how matter doesn't interact with gravitational waves, but I am still somewhat unsatisfied with this since you may think that the Earth will bounce after a wave passes creating more waves of its own (here is another aspect where this representation of spacetime is not perfect).

FYI: A better 3-dimensional representation of spacetime is shown in this clip from the American Museum of Natural History's short documentary called Gravity: Making Waves (which can be seen in its entirety on my Viewing Fun! page).  This animation shows a grid-like scaffolding filling space in which there is a depression caused by mass.  While it still isn't a perfect representation of spacetime, it is much better than the trampoline approximation above.

The Lunar Eclipse Explanation:

Recently, I thought of another more intimate example that most of us can identify with: a total lunar eclipse (which I have also blogged about).  This is a situation where the Sun, Earth, and Moon line up in that order so that the Moon is completely in the Earth's shadow:

Image from Wikipedia

When the Moon is completely in the Earth's shadow (or the umbra in the diagram above), a viewer on the Moon would not be able to see any part of the Sun.  If the gravitational field from the Sun were blocked by the Earth, then the Moon's orbit would appear to change.  Since there is no change in the Moon's orbit during a total lunar eclipse, then the Earth does not block the Sun's gravitational field.  By extension, the Earth also would not be able to block any changes in the gravitational field (which are gravitational waves).  If you are familiar with physics, this is an application of the principle of superposition.


Great!  But Why do We care?

Since mass does not absorb or reflect gravitational fields, the Universe is transparent to a gravitational wave.  This is a huge advantage when using gravitational waves to make astronomical observations since nothing can block our view of a gravitational wave!  If you have ever seen the our own Milky Way galaxy in the sky on a clear, dark night, you've seen the billions and billions of stars that live in our "backyard": 

Fish-eye mosaic of the Milky Way galaxy as seen from Chile.  [Image from Wikipedia]

While this is beautiful, it also it almost impossible to see past all the stars and dust there to observe what is behind our "backyard".  We will be able to see right through the Milky Way with gravitational waves! 

P.S.  We can also detect gravitational waves from the other side of the Earth with LIGO since gravitational waves can travel through matter.  Read more about this in this previous post (under the subheading of "Why are there 2 LIGOs?")!

What Is a Higgs Boson?, What Did CERN See?, and Why It's a Big Deal!

This is my disclaimer - I AM NOT A PARTICLE PHYSICIST!  Therefore, this subject does not fall into my realm of expertise.  However, I do have a very basic training in the physics behind all of this so I would like to share with you a little bit about why all of us physicists have been so excited of late...


WHAT IS A HIGGS BOSON?

The Higgs boson (regular Wikipedia entry, Simple English Wikipedia entry) is the elementary particle that gives matter mass.  Many of us have probably heard about Einstein's famous equation:

This image is taken from Wikipedia.

While this equation is famous, the true meaning behind what it means is often not fully appreciated (I used to see it and simply think "Einstein!").  It means that mass can be converted to energy and energy can be converted to mass, also known as the mass-energy equivalence.  The energy, E, from an amount of mass, m, is equal to the mass multiplied by the speed of light, c, squared (c² = c*c, c is about 670,616,629 miles/hour).  If you were to convert 1 oz of matter into energy, you would have about 2,500,000,000,000,000 Joules of energy and this would keep a 100 W light bulb lit for over 807,389 years!  So, a little bit of matter can be converted into an immense amount of energy!  It is this conversion of mass to energy that makes nuclear weapons so destructive.

But, if we convert energy into mass, where does this mass come from?  The Standard Model, which is the working description of how the fundamental particles interact (I talked about this in my post discussing gravitons), says it comes from the Higgs field.  This is a field similar to the electric field and the magnetic field (more on fields in general here).  At the instant after the Big Bang, all particles moved at the speed of light (c from above) since none of them had mass because there was no Higgs field.  In the next instant (about a trillionth of a second later), the Higgs field came into existence and produced a resistance to particles based on what they were made of.  This resistance manifests itself as mass: the slower a particle moves through the Higgs field, the more massive it is.  The Standard Model also allows fields to manifest themselves as particles (the photon is the particle associated with the electric and magnetic fields).  Therefore, this Higgs field should also manifest itself as a particle and we call it the Higgs boson.

The only particle from the Standard Model that has not been detected is this Higgs boson.  (Note that gravity is not described by the Standard Model.)  This is because the Higgs boson is very massive for a fundamental particle at about 133 times the mass of a proton.  The amount of energy conversion needed to produce this mass is much larger than we have been able to create in the past.  That is, until CERN built the Large Hadron Collider (LHC)...


WHAT DID CERN SEE?

View of the CMS experiment [note the person near the center] (© CERN)

CERN is the home to several experiments including CMS and ATLAS.  Both of these experiments smash together protons with very large energies.  The protons and their energy can change into a Higgs boson (if there is enough energy).  The Higgs boson decays (changes into something else) almost immediately, so the LHC experiments look for the Higgs boson's signature in the resulting particles.  There are 5 pairs of particles that result from the decay of a Higgs boson, including 2 photons.

Both CMS and ATLAS saw the Higgs signature in 2 of the 5 different resulting decay pairs.  Only CMS had sufficient data to look for all 5 kinds of decay pairs and saw with high certainty signatures in 4 of the pairs.  More research is needed for the signature CMS didn't see.

Diagram of the ATLAS experiment [note the people on the bottom left] (© CERN)

WHY IT'S A BIG DEAL!

The official conclusion is that CERN has indeed observed a Higgs-like particle.  "Higgs-like" does not mean that they are unsure if they found what they were looking for.  Instead, it appears that the Higgs boson they observed has more properties to it than the Standard Model predicted.  The LHC has found what it is looking for as well as hints that there is new physics to be discovered.

So this is the big deal: the population of the Standard Model is complete but the model itself doesn't appear to describe everything.  That is something we knew before, but now we are seeing it with the apparent complication in what was and wasn't observed in the discovery of the Higgs boson.

I am a physicist because every time you discover something new, not only do you understand the Universe better, but you have even more exciting questions to answer!  Soon enough, it is going to be gravitational waves stirring up excitement like this and I am going to be in the midst of it all!


Side Note:
IT'S NOT THE 'GOD PARTICLE'

The Higgs boson is sometimes referred to as the "God particle," especially by the media.  However, it has nothing more to do with God than any other particle in the Universe.  The origin of this misnomer is a book by Nobel Laureate Leon Lederman titled The God Particle: If the Universe Is the Answer, What Is the Question?.  Likening the Higgs boson as a God particle refers to it being the origin of all matter's mass.  Physicists (like me as well as Lederman himself) generally dislike this nickname since it places much more import on this particle than it deserves.  But above that, it is offensive to people of faith and makes us look like we are trying to replace God.  We aren't. 


Want More? ...
Watch the announcement seminar
Read the official CERN press release

Q: What Do Gravitational Waves "Sound" Like?

Okay, this isn't a question that I usually get asked but the answer to this question is the basis of my answer to questions about how we can determine information about what produced a gravitational wave from the signals we detect.  So, how do we do that?

One convenient feature of LIGO is that it is most sensitive in the frequencies that the human ear could hear if gravitational waves made sound - but they don't.  I can't stress this enough: gravitational waves do NOT make sounds since a sound waves are fundamentally different from gravitational waves.  But, if we take the data we gather from LIGO of a gravitational wave, we can put that signal through speakers and convert them into sound.  In this way, LIGO is very much like a gravitational-wave radio...


LIGO AS A GRAVITATIONAL-WAVE RADIO

Radio stations broadcast radio waves at a specific frequency (this is the number that you tune your radio to) and music is encoded onto this wave.  Whereever you are right now, you are most likely surrounded by radio waves from numerous stations but you can't hear radio waves or the music that is encoded onto them.  To hear this music, you need to have an instrument that can detect the radio waves, decode the music from them, and turn this signal into sound using a speaker.  Now, you can hear the music.

LIGO is a completely passive detector (meaning we just wait for something to happen, we cause nothing that we can detect other than noise) just like your radio is passive (it can't create music).  We wait for a gravitational wave to pass by Earth, and if it is strong enough and in the frequency range that we are sensitive to, then LIGO will detect a signal.  From that signal, we can extract information about what made the gravitational wave, like a radio decodes the music from the broadcast radio waves.  Once we have detected the signal, we can put that signal through speakers to convert it into sound.  Just like a radio, it is the speakers that make the sound and not the detector.  Since LIGO is sensitive to frequencies that are in the same ranges of sounds we can hear, we can hear the gravitational-wave signals when put through a speaker.  Now we can extract information about what made the gravitational wave just like we can hear the different instruments and voices in music.


LIGO'S SENSITIVE FREQUENCIES = AUDIBLE FREQUENCIES

Initial LIGO's most sensitive range (as we were before we started our current upgrades) was between about 60 Hz to 800 Hz.  This corresponds to the lowest note on a cello (click here to hear what 65.41 Hz sounds like) to the lower notes on a piccolo (click here to hear what 523.25 Hz sounds like), respectively (according to Wikipedia).  Once Advanced LIGO is complete and operating at sensitivity, it will be more than 10x as sensitive as Initial LIGO and its most sensitive region will be between about 20 Hz to 2000 Hz (this is the range that produces at least 10x the sensitivity of the sensitive range noted for Initial LIGO).  This corresponds to the lowest frequencies humans can hear (like the lowest note on a tuba) which is usually felt more than heard to a little below the highest note on a flute (click hear to hear what 2093 Hz sounds like).  LIGO's sensitivity to different frequencies are shown graphically below:

LIGO sensitivity vs. frequency (see this post for a description of how to interpret this plot).
Click on the graph to see a larger image.

Recall from a previous post that it is because LIGO is most sensitive to the audible frequency range that we cannot detect gravitational waves from the Moon, Sun, and planets; they produce gravitational waves at much lower frequencies.


THE "SOUNDS" OF DIFFERENT KINDS OF GRAVITATIONAL WAVES

We can tell just from what a gravitational wave "sounds" like what category it is classified as; there are 4 major categories:

1. Inspiral gravitational waves: two massive objects orbiting each other faster and faster as they get closer together and eventually merge into one.  Pairs of neutron stars, black holes, or the combination of the two are prime candidates for detection.
     ⇒These waves are expected to sound like a "chirp" (click here to hear the example in the plot below):





2. Continuous gravitational waves: a distorted object rotating about its axis with a constant frequency (the Earth rotates with a very constant frequency of once per day).  A neutron star rotating rapidly with a "mountain" on it are prime candidates.  ("Mountain" is in quotation marks because it is a deformation as little as a few inches high on the nearly perfectly spherical neutron star.)
     ⇒These waves are expected to sound like a single tone (click here to hear the example in the plot below):





3. Stochastic gravitational waves: many weak signals from different sources combining into one "jumble" of a signal.  Relic gravitational waves from the Big Bang are expected to be candidates for detection.
      ⇒These waves are expected to sound like static noise (click here to hear the example in the plot below):





4. Burst gravitational waves: these waves are short duration and from unanticipated sources or from known sources where we can't be sure what the gravitational waves will "sound" like.  I like to call these the gravitational waves that go 'bump' in the night.
      ⇒These waves are expected to sound like 'snaps', 'crackles', and 'pops' (click here to hear the example in the plot below):

While is is great to see and hear the differences between the different kinds of gravitational waves, it is harder to see how we can glean more specific information about the thing(s) that made the gravitational wave.  The answer is that we can use general relativity to predict what kinds of signals ("sounds") a certain situation will create.  Below is a movie by Steve Drasco (Caltech/CalPoly) showing the sped up evolution of a body 270 times the mass of our Sun orbiting and finally merging with a supermassive black hole 3 million times the mass of our Sun.  The movie starts one year before the two objects merge and the bottom of the frame shows a graph of the gravitational waves while the majority of the frame shows the orbit of the system.  As you listen, you can hear how the tone changes into the chirp that is characteristic of this kind of system (the movie is ~13 MB so it may take a minute or two to load):

 

By studying the predictions of what different gravitational waves will "sound" like, we can translate a detected gravitational wave into information on the system that made it.


DO WE ACTUALLY LISTEN FOR GRAVITATIONAL WAVES?

Yes and no...  The option to listen to the data as it is collected is available to scientists working in the LIGO control room.  I've done it but I don't make a habit out of it since almost all of what LIGO detects is small vibrations from our environment.  You can listen to real LIGO noise by clicking here (if you carefully listen all the way to the end, you can hear a fake inspiral chirp that has been added to the data - you may miss it).  Since what you predominantly hear sounds like static, it can lull you to sleep which isn't advisable when you are the responsible scientist on duty!  Also, almost all gravitational waves will be too weak to hear with our ears which is why we mainly analyze data using sophisticated data analysis techniques that have been specially designed to search for each of the four categories of gravitational waves.  (This is what I do for a living!)

I also wrote in March 2011 about a fake signal that was placed (injected) into the LIGO data to test if our data analysis techniques could really detect a gravitational wave if there was one.  This was a blind test (called the "Big Dog" due to its apparent location in the constellation Canis Major) meaning that only a few individuals knew about this fake signal and the rest of us were left to find it and interpret its results.  While we did not detect this signal by listening to it, it can be heard in both the LIGO detectors (about 17 seconds into the recording linked below).  This is real LIGO data and the sound may be VERY LOUD - so turn your volume down before you play it and then adjust it!
     ⇒Click here to hear the data around the blind injection for LIGO Hanford, WA.
     ⇒Click here to hear the data around the blind injection for LIGO Livingston, LA.*
          *Note that there is a audible instrumental "glitch" in the Livingston data about 8 seconds into the recording; this is unrelated to the injection.

While it is difficult to hear gravitational waves that will be buried in detector noise, there is no denying that the human brain is very effective at breaking sounds down into their individual components.  A recent Physics Today article titled "Shhhh.  Listen to the Data" discusses the advantages of humans listening to data and features a discussion of this application to LIGO.  Also, if you want to test your ear's talent at "hearing" gravitational waves, there is a fantastic website called Black Hole Hunter which places black hole gravitational wave "sounds" (like the system in the movie above) into simulated data and tests if you can discern the signal.  I've spent many an hour playing with this and even use some of the cell phone ringtones they've made (also available on the Black Hole Hunter site).

*** If you are interested in more gravity games, see my Gravity Games page (link here and under the blog banner)! ***


WANT TO HEAR MORE?

There are some great sites that feature the "sounds" of gravitational waves.  Here are a few of my favorites:

• Black Hole Hunter
• Scott Hughes' (MIT) page of gravitational wave sounds (and a more out of date one)
• black-holes.org page of gravitational wave sounds