But what about an object flying by a black hole (or any other massive object) instead of being in a nice stable orbit (like the Earth is in the previous example)? This makes things a little more complicated, so I am going to let go of telling a love story. That being said, there will be more equations here, but like the previous love story post the equations will only serve to help tell the story and we will not be using any numbers.
THE FATE OF A COSMIC WANDERER
Instead of looking at the universal gravitation law, we are going to look at how a passing object comes to be in orbit, or not, around another object (this governed by Kepler's laws of planetary motion). To keep things simple, let's assume that the moving object has much, much less mass than the object it's passing (this is so that we can ignore the motion of the big object due to its gravitational attraction to the passing object). Basically, picture something small whizzing through space (I'll call this the small object) that passes by a star or black hole (I'll call this the big object). It is now safe to assume that any motion caused by gravity is going to be seen in the small object.
IT'S ALL ABOUT THE SPEED
The one factor that completely determines the fate of the small object is its speed. If this speed is great enough, then the small object will be able to escape the big object, though its speed and direction will have changed. The minimum speed at which the small object will not be captured into an orbit is called the escape velocity:
Here, we see that the escape velocity, ve, changes as the square root of 1/distance (1/r) between the objects' centers. That means that the closer the small object is to the big object, the more speed it must have in order not to get caught by it; the farther away, the less speed it needs to escape. 2GM is a constant value and never changes; G being the universal gravitational constant and M being the mass of our big object.
ORBITS AND ELLIPSES
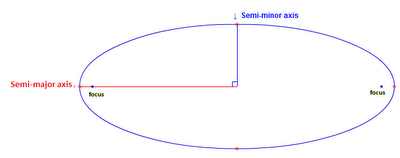
Any speed less than the escape speed and the small object will be captured by the big object and will likely start orbiting the big object (or collide with it, we'll get to that later). Let's say that we are traveling at a speed less than the escape velocity. Kepler's laws of planetary motion (which are a consequence of gravitation) provide that the shape of the orbit is an ellipse (an oval shape). Instead of having one center like a circle does, an ellipse has 2 each called a focus. A classic way to draw an ellipse for yourself is to put two pins into a piece of paper, put a loop of string around the pins, place a pen in the loop and pull the loop taut. The shape that you draw doing this is an ellipse:
 |
| [Image from: Wikipedia] |
Here, each pin is a focus. This is what having 2 "centers" means - if you were to draw a shape using this same method but using only one pin, then you would draw a circle (the pin being the true center). When talking about an orbit of a very massive object and much smaller object (like we have in this example, or like the Earth orbiting the Sun), the more massive object will be located at a focus and there isn't anything at the other focus.
The speed of the object determines the shape of orbit:
Here v is the speed of the orbiting object (which is less than the escape velocity), μ is a constant (G times the mass of the big object), r is the distance from the objects' centers when the velocity is measured, and a is the semi-major axis of the ellipse (the distance between the midpoint of the foci and the farthest point of the ellipse).
 |
| [Image from: Wikipedia] |
STARSTRUCK!
Under what conditions does the small object collide with the big object? So far it sounds like the small object is either going to escape the gravitational pull of the big object or start orbiting it. Can a black hole (assuming it's our big object) ever "swallow" anything? Yes, indeed, but only under certain conditions...
To determine the conditions for an object to be swallowed by a black hole or collide with a star, we need to realize that neither of these objects is a nice point as we have been treating them (well, the singularity inside the black hole is a nice point, but more on that below). Instead, objects occupy a volume and the points we were considering were really the center of mass of the object (approximately the actual center for a spherical object). So, the small object will collide with the big object if the radius of the big object is more than the distance of closest approach of the small object's orbit. This distance is called periapsis and is the distance along the red line (the semi-major axis) between the ellipse (orbit) and the focus (the big object) in the previous figure. If a star has a radius of this or more, then the small object will slam into it.
NOTE: This scenario for collision (and the one for merger with a black hole below) assumes that the objects only interact through gravity. That means that there is no consideration here for other forces like the interactions of the objects' magnetic fields (if they have them) or resistance from the matter and radiation that stars tend to spew out.
HUNGRY, HUNGRY, BLACK HOLES
But what about the specific case of a black hole? I mention that there is a point-like singularity in the black hole where all the mass is located. How do we determine the shape of the whole black hole? First, consider why a black hole is called "black"; because the gravity inside of it is so strong that the speed of light is less than the escape velocity (now you can think of our small object as a photon of light). Since nothing can travel faster than the speed of light, nothing can escape a black hole. So we define the edges of the black hole to be the radius at which the escape velocity equals the speed of light. This radius is called the event horizon. Therefore, an object (even a photon) will merge with a black hole when the distance of closest approach of its orbit is equal to or less than the event horizon.
Now that's what I call "starstruck" lovers! Get it? The small object strikes the big object which could be a star... Okay, I know it's lame, but that's why I'm a physicist and not a comedian (though I do try!).
♥ Speaking of love, happy anniversary to my husband, Derek, who is always nice enough to proofread these posts. We've been together for 16 years, married for 9 and looking forward to many more! ♥


