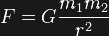Second Anniversary of the First Detection and a New Job!

While posts here have been long awaited, I've been busy doing research, teaching, and changed my job!  I've just started a new job as an assistant professor at Villanova University and an academic job search is quite intensive (perhaps I will write about finding a faculty job soon).  Also, I've been writing some other things.  I've written a TED-Ed video/lesson on gravitational waves and it premiers today (you can view it here), I have a PhysicsWorld Discovery text on "Gravitational Waves" coming soon, and have written a few other things here and there.  So, now that I've moved from Baton Rouge to the suburbs of Philadelphia, I have some time to talk with all of you again.



ANNIVERSARY OF GW150914:  WHERE IS IT NOW?

Today is the second anniversary of the first detection of gravitational waves.  That got me thinking of about where the front of that wave is now...

The colored area on this map shows the most probable source of the detected gravitational wave where red is more likely than purple.  The location is shown against a map of the night sky centered on the Milky Way galaxy with constellations outlined.
[Credits: NASA Deep Star Maps (Visualization Credits, Ernie Wright (USRA): Lead Animator, Tom Bridgman (GST): Animator) by NASA/Goddard Space Flight Center Scientific Visualization Studio with constellation figures based on those developed for the IAU by Alan MacRobert of Sky and Telescope magazine (Roger Sinnott and Rick Fienberg), and the source location based on Gravoscope screen grabs (LIGO & Nick Risinger, skysurvey.org), all in galactic coordinates. Composition by University of Florida / S. Barke.]

The source of GW150914 was from the general vicinity of the constellations Volans and Carina.  That means that it is traveling towards the stars in the constellation Draco.  It hasn't encountered much.  Since it has traveled a distance of 2 light years from Earth, it is still in our Milky Way galaxy (the radius of the Milky Way 60,000 is ly and its disk is 2000 ly).  It has not encountered any other stars (the closest star in Draco is Struve 2398, a binary system of red dwarf stars 11.6 ly away) and therefore no other planets.  That means that no other life forms have detected GW150914 and won't reach Struve until early 2027 (give or take for the error in our understanding of its distance).


THE THIRD DETECTION: GW170104

Since I wrote last, we announced the discovery of a third detection of gravitational waves from another binary black hole system dubbed GW170104.  A black hole 32 times the mass of our Sun merged with another black hole 19 times the mass of our Sun resulting in a single 49 solar mass black hole after radiating away 3 solar masses in gravitational waves.  Among other things, this detection helps to fill in the range of masses we've observed; gaps would imply that there is something preventing the formation of those kinds of systems and that would be unexpected.

Graphic representation of the known stellar mass black holes observed through X-ray observations (purple) and gravitational waves (blue).  [credit: LIGO/Caltech/MIT/Sonoma State (Aurore Simonnet)]

TESTING GENERAL RELATIVITY 

This system originated from about 3 billion light-years away: farther out in the universe than any of our previous detections.  Using a gravitational wave that has traveled such a distance allows us to test a part of general relativity that we haven't been able to before: do gravitational waves disperse?  For example, when white light enters a prism, the different colors (frequencies) of light travel at slightly different speeds causing them to separate or disperse.  General relativity predicts that different frequencies of gravitational waves should not disperse.  There are alternate theories of gravity that make predictions of how dispersion will affect a gravitational wave.  We compared our observation to standard general relativity and the alternate theories' predictions and found our observations to be consistent with general relativity.  That is, we did not observe any significant dispersion of our gravitational wave!  We've also done all of the tests of general relativity that were done for the previous detections and this gravitational wave continues to affirm that general relativity is correct.

MEASURING SPIN TO INVESTIGATE BLACK HOLE FORMATION

Artist's conception shows two merging black holes similar to those detected by LIGO. The black holes are spinning in a non-aligned fashion, which means they have different orientations relative to the overall orbital motion of the pair. LIGO found hints that at least one black hole in the system called GW170104 was non-aligned with its orbital motion before it merged with its partner. Credit: LIGO/Caltech/MIT/Sonoma State (Aurore Simonnet)

We also were able to investigate the spin of the black holes.  For as mind-blowing as a black hole is, it is completely described by three numbers: 1) its mass, 2) its spin, 3) its charge (this is postulated by the no-hair theorem).  Since we believe the electric charge of astrophysical black holes to be negligible, physicists get very excited about the mass and the spin.  The mass is not too hard to measure (we can get that pretty accurately from the waveform shape and frequency evolution), but the spin is all in the details of the signal which makes it more difficult to estimate.  But we always still mention it because any information we get about it will tell us more about the other half of the back hole's story.

For this detection, we were able to extract information about how the combined spin of the black hole system compares to the direction of its orbital angular momentum.  Basically, does the direction the effective spin of the black holes (on their internal axes) go in the same direction as their orbit?  For example, the Earth spins on its axis in the same direction as it orbits the Sun, so this is a positive alignment, but the Earth's axis is tilted so it isn't a perfect alignment.

If most of our black hole systems have small misalignments that would support their formation through something we call "common envelope evolution" (I wrote about this here), which is a complicated way of saying that the stars that formed the black holes were always paired together and once they both died you end up with a binary black hole system.  The interactions between those original stars will cause their spins to align giving the resulting binary black hole system only small misalignments.

Another formation mechanism for binary black holes is that they just happened to pass one another while drifting through space and became gravitationally bound together (this is called dynamical assembly).  We expect things like this to happen in dense stellar clusters or near the centers of galaxies.  Since these would have had no interaction with each other before they became a system, we expect random spin alignments from the black holes.

Ultimately we found that our system likely had a low total spin and was likely not aligned with the orbital angular momentum of the system.  It is also possible that our black holes had no spin to begin with.  So this isn't definitive, but we are starting to assemble the story of how black hole systems like this form.


THE BIG PICTURE

With this discovery, we are adding to our understanding of the universe and testing general relativity in ways we've never been able to before.  The importance is that LIGO is truly operating as an observatory (that's what the 'O' in LIGO stands for after all) and building a database of observations.  In astronomy, you can never make a single observation and understand a system's history.  You need to take a large sample of observations from similar systems and find out what the patterns are.  That's how we understand how stars evolve since a human life, or even all of human existence, isn't long enough to have followed a single star's life cycle.  But because we have observed many stars in different stages of their lives we've discovered patterns.  That's how we know that the black holes we just observed are the collapsed corpses of the extremely massive stars.  Now we can collect observations of many of these black hole systems to learn more about black holes in general and how these pairs of black holes form.

Merry Christmas, LIGO: Another Gravitational Wave!

WE DETECTED ANOTHER GRAVITATIONAL WAVE!

On the evening of Christmas day 2015, at 9:38 pm CST (3:38 am UTC) at the LIGO Livingston Observatory in Louisiana, another gravitational wave signal was recorded.  1.1 ms later, the LIGO Hanford Observatory in Washington state also picked up the same signal.  70 seconds later, the supercomputer that runs analyses on the near real-time data noticed that there was something special in the data and sent out emails and text messages that some of us affectionately call the "Bat Signal".  This goes out to scientists primarily to summon those who evaluate candidate gravitational wave events to determine if this event should be shared with traditional astronomers (i.e. ones with telescopes).  I am on the list because I am interested in keeping up on the latest results.  I remember exactly where I was: I was in my room at my mother's house outside of Pittsburgh changing clothes after getting back from visiting the in-laws (who live within a few miles of my family's home) for Christmas.  I looked at the event record and saw that this was an extraordinary candidate gravitational wave in that its statistical significance was high but the signal wasn't as obvious in graphs as the first detection in September was.

It was decided to send out the location of the possible detection to traditional astronomers and the emails started flying discussing the evidence that this was a true detection.  It was determined that the preliminary information on the signal warranted starting the detection checklist - the large-scale investigations that try to disprove that the signal is real.  Only after a candidate passes every test and has a high statistical significance is it accepted as a detection.  The same checklist that was applied to the first detection, labeled GW150914, was applied to this candidate as well.  Once this Christmas detection was verified, it was labeled GW151226 (the number reflects the UTC date that the gravitational wave was discovered) although we had nicknamed it the "Boxing Day Event" before the verification.

(Below I will often refer to GW150914 as the "first detection" and GW151226 as the "new detection".)

Read the paper on the detection here.


THE SIGNAL & THE SOURCE

The signal is similar to the first detected gravitational wave (GW150914).  We call this kind of signal a "chirp" because initially it has a low frequency which increases over time as does its amplitude.  You've heard signals like this before if you've ever hear a slide whistle increasing in tone.  The increase in tone reflects the increase in frequency and the loudness of the whistle represents the amplitude.  The signal we detected starts at about 35 Hz (close to the frequency of the sound made by the second black key from the left on the piano) and reaches its highest frequency at about 450 Hz (very close to the A above middle C if you convert this signal into sound).

Graph of the 1-second signal of GW151226.  The red line is the prediction of what a gravitational wave from a 14.2 and 7.5 solar mass black hole merger would look like and the grey area around it is the signal that LIGO recovered from its data.  The zoomed in portions allow you to get a better look at hour the prediction (in red) and the actual signal (in grey) compare.  At the end of this signal, the frequency and amplitude both go up.  The two black holes merge at the point where the amplitude of the signal is the highest (seen in the zoomed data to the far right).

The plot above shows what we detected in our data compared to the predictions of a pair of black holes orbiting each other and merging into one.  So this is similar to the last detection in that this is also a pair of stellar-mass black holes (formed from the death of extremely massive stars) but different because the masses of these new black holes are less than the first detection.  Here, our newly detected black holes are 14.2 and 7.5 solar masses where our last detection was 36.2 and 29.1 solar masses.  That makes this signal weaker than the last (the peak amplitude of this new signal is about 1/3 that of the first detection) but we are able to observe more orbits of the system here.  We see about 27 orbits of these new black holes (corresponding to the 55 cycles of the gravitational wave we see in the figure) where we only saw about 5 orbits (or 10 cycles) in the first detection.  It is interesting to note that lower mass black hole pairs will merge at higher frequencies than higher mass black holes.  This means that the signal will stay in LIGO's most sensitive frequencies longer and that is reflected in what we see here.  This new detection's signal is about 1 second long while the first detection is less than a half second long.

So, what did this new detection look and sound like?  As far as what it looked like, there was no light that we are aware of that was produced from this system.  But we can visualize the black holes as they orbit around each other and track the corresponding progression through the signal to the merger.  [Credit: SXS Collaboration/www.black-holes.org]:

We can also "listen" to gravitational waves by taking the signal, and converting it into sound through your speakers.  Below is a comparison of what the new detection "sounded" like compared to the first detection.  The actual "sounds" are quite low in tone so that they sound more like thumps.  We also have shifted the sounds up to a higher tone so that you can hear more of the detail in the signals.  That will play after the original lower tones.  The background graph shows how the frequency changes on the vertical axis (you will see that it increases for both signals) as time progresses on the horizontal axis:

The next question is where in the sky are these black holes?  We primarily determine this using the delay in detection time between the two detectors.  When the delay is large, there is a smaller area in the shape of a ring on the sky where the gravitational wave could have come from.  The detection delay for the new detection is much shorter than the first detection, so our uncertainty is going to be larger.  Below is an illustration of the areas on the sky where the new detection (the area to the left) and the first detection (the area to the right) are likely to have come from.  Note that for the new detection on the left, there is another similar area on the opposite side of the sky that cannot be seen in this image.

The location of both the new GW151226 detection (on the left) and the first detection, GW150914 (on the right).  These are pictured on a star map (you can see the center part of the Milky Way galaxy on the left and extending right).  There is another similar area for the new detection on the opposite side of the sky (not pictured here).  The outer purple area is where we are 90% confident where the sources are located.  The inner circles each have decreasing certainty.

We will be better able to determine the location of a gravitational wave source on the sky when we have more than two detectors in operation.  Fortunately, Advanced Virgo has completed their upgrades and is currently testing their new detector.  LIGO's next observing run is expected in the 4th quarter of this year and Advanced Virgo will likely join the search before the completion of that run.  When we detect more gravitational waves (which we expect since we will be even more sensitive than we were for the two detections we have already made and the run will be longer in duration) together with Virgo, we will know even more about what it is that we are seeing.

This is an exciting time to be a scientist!

Read the official LIGO "Science Summary" on this new detection, GW151226.

The Source of GW150914: Stellar Mass Black Holes

On September 14th, 2015, LIGO made the first direct detection of gravitational waves.  This event is labeled GW150914 (referring to the year, month, and day of the detection).  The objects that produced the GW150914 were a pair of stellar mass black holes that orbited each other and gradually moved closer and closer together over the course of eons.  The closer together they became, the faster they orbited around each other and the stronger the gravitational waves produced.  LIGO detected the last 0.2 seconds of these stars orbiting until they became so close they merged into a single black hole.

While we saw the death of this paired (binary) system, we didn't get to observe other parts of its life.  Where did these black holes come from?  To answer this question, we need to apply what we know about stellar evolution.


STELLAR MASS BLACK HOLES ARE CORPSES

There are several classes of black holes, determined by their mass and how they were formed: stellar mass black holes, intermediate mass black holes, and supermassive black holes.  For stellar mass black holes, they formed when the most massive of stars (more than 15-20 times the mass of our Sun) run out of nuclear fuel and gravity takes over and collapses the star.  For smaller stars, this collapse stops when the pressure from inside the atom (neutron pressure) equals the pressure from the gravitational collapse.  But for these more massive stars, there is no pressure that can stop the collapse and a black hole is formed.  It is in this way stellar mass black holes are the corpses of the most massive stars (but these kinds of black holes are among the least massive).  The newly merged GW150914 black hole now holds the record for the largest stellar mass black hole known.

There are several theories about how this happens... Sometimes this collapse is accompanied by an explosion called a hypernova and is believed to be the source for a kind of gamma-ray burst.  Sometimes the gravity of the collapsing star is so great that all of the matter and light gets sucked into it even if there was a hypernova-like explosion.   


THE EVOLUTION OF THE GW150914 SYSTEM

But how did two stellar mass black holes come to be paired together?  A likely explanation is that they also lived their lives together as a binary star system.  This is very common as it is estimated that about 1 out of 3 stars are in systems of 2 or more stars.  This binary system would likely have formed together and lived their entire lives paired.  The more massive of the 2 stars would have died first since the more massive the star, the faster it burns through its fuel.  Once the nuclear fuel ran out, the more massive star collapsed into a black hole making the system a star/black hole system.  Eventually, the second star would run out of fuel and collapse into a black hole as well making our stellar black hole binary system.  These black holes would orbit for eons before they were close enough to merge and produce the gravitational waves LIGO detected.

In a recent paper (see reference below or read it here), simulations of millions of stars with different material compositions (specifically metalicity which, to an astronomer, is anything that isn't hydrogen or helium; the Sun is 2% 'metal') were simulated and some produced similar outcomes to what we observed.  What was found was that there were similar characteristics for the stars the went on to resemble the GW150914 binary system and this gives us estimates on the time needed for each stage in the system's evolution from birth to the gravitational-wave-generating merger.

The two stars were born about 2 billion years after the Big Bang and were each somewhere between 40 to 100 times the mass of our Sun.  These low metalicity stars (only about 0.06% 'metal') orbit each other as stars for about 4 million years until the more massive one collapses into a black hole.  The now star-black hole system orbit each other for another 1.5 million years until the other star collapses into a black hole.  Both of these stars were massive enough that there wouldn't have been a hypernova-like explosion for either of them; any material ejected would have fallen back into the black hole.  Our new black hole binary system, which is just the corpses of once very massive stars, now go on to orbit each other for over 10 billion years - that is 1000 times longer than the either star was a alive.  At the end of that time, they merge and produce the gravitational waves that LIGO detected 1.3 billion years later when they arrived at Earth.


WHAT WILL HAPPEN NOW?

The short answer: nothing.  This new single black hole is spinning (it is the first detection of a Kerr rotating black hole) but its shape and center of mass are not moving in a way that will ever produce gravitational waves again.   Gravitational waves are also the only way this system would ever have been detected since there wasn't any matter (like dust or gas) to fall into the black holes and generate X-rays.  We will never be able to observe this black hole again.

Of course, there are extremely unlikely events like another black hole flying by and crashing into it...  That may make new gravitational waves for us to see (but I wouldn't hold my breath).


Reference:

K. Belczynski, D. Holz, T. Bulik, R. O'Shaughnessy, "The origin and evolution of LIGO's first gravitational-wave source" arXive e-Print: 1602.04531 (2016).

LIGO Makes the First Direct Detection of Gravitational Waves

On morning of 14 September 2015 at almost 4:51 am in Louisiana (09:50:45 UTC) the LIGO detectors in Livingston, LA and Hanford, WA detected a gravitational-wave signal we've labeled GW150914 (based on the date).  The online (near real-time) data analyses alerted scientists about 3 minutes later that there was something of substantial interest in the data.  While vetting this signal (that only lasted about a half of a second) took a substantial amount of time, it opened the new field of gravitational-wave astronomy.  We had not only made the first direct detection of gravitational waves but we also made the first direct detection of a black hole binary (pair) system and proved that these kinds of systems really do exist (it was contentious because the formation of one of the black holes was expected to have destroyed the star that would have made its partner).

At the time of the posting of this blog, the press conference making the announcement is going on and I am working the satellite event being held at the Livingston Observatory.  I will be sure to update this post with the link to the recording or the announcement later (update: see the bottom of this post).  There is too much to talk about in just this post, so I am going to keep this to the basics: what did we see and what does it mean?  I will be doing a series of posts about what we did to make sure that this is a real gravitational wave, the astrophysics of the source, how we detected it, the creation of black holes and why finding a pair like we did is important to astronomy.

Update: Read the Physical Review Letters journal article here.


THE SIGNAL

This gravitational-wave detection was seen as a common signal between the two LIGO sites:

This image shows the data (top row), signal (middle row), and what's left over after the signal is subtracted from the data (bottom row).  Detailed discussion on each image is provided below.

What you see here is a series of images (above and in detail below) that picks apart the signal that was detected.  In the left column is information focusing on the Hanford Observatory and on the right the Livingston Observatory.

TOP ROW:

The vertical (Y-axis) units are strain with a scale of 10^-21.

In the top row is the signal that was seen.  However, this is not the raw data as it was collected.  What you see here is data that has been filtered to 1) reduce noise and 2) to include only frequency components that are around the frequency range of the signal itself.  The red graph on the left is the signal as seen at Hanford and on the left the blue trace is as seen at Livingston.  For comparison, the light red line under the blue Livingston line is the Hanford signal that has been shifted in time to account for the travel time between detectors and flipped (multiplied by -1) to match the orientation of the arms (the arms of each site have a opposite orientation compared to each other so the positive signal in one detector will be negative in the other).  The common signal can be seen with the noise in this comparison.

MIDDLE ROW:

The vertical (Y-axis) units are strain with a scale of 10^-21.

These plots compare the signal predicted by numerical relativity (which are results of computer simulations where the predictions of general relativity cannot be solved by in explicit mathematical expressions) for a pair of black holes with one mass 36 times the mass of our Sun and the other 29 times.  (The red line in the left plot for Hanford and the blue line on the right for Livingston.)  Beneath each of these lines are grey shadowed areas that show the signal as detected from actual LIGO data with two different independent data analysis methods (wavelet and template).  Here again, we can see that the predictions and observations match well.

BOTTOM ROW:

The vertical (Y-axis) units are strain with a scale of 10^-21.

These are plots of residual signals which are the noise that this left behind when the gravitational-wave signal is removed.  Seeing that there is no pattern left in these plots supports that what was seen was a real common signal - a real gravitational wave (this is necessary for a gravitational wave detection but not sufficient - the extra investigations performed will be the subject of a future post).


THE SPECTROGRAM

A powerful tool in signal analysis is breaking up a signal into its frequency components in a graph called a spectrogram.  It allows us to see how much of a signal is made up different frequencies at different times.  If you can hear, then you do this everyday.  It is how you are able to pick apart the sound of a tuba from the sound of a flute when you listen to a symphony.  Both are playing at the same time, but you don't confuse their sounds as coming from anything else.

Below is the spectrogram of this gravitational wave detection:

The horizontal (X-axis) is the progression of time (like above) and the vertical (Y-axis) is showing the contribution of each possible frequency.  The more yellow at a frequency, the stronger that frequency's contribution to the signal at that time.  Our gravitational wave starts at a low frequency (about 35 Hz) and increases to higher frequency (about 250 Hz) near the end of the signal.  This is similar to a signal a slide whistle increasing tone would produce.


WHAT WOULD THIS SOUND LIKE?

As I've mentioned in a previous post, the frequencies of gravitational waves that LIGO is sensitive to would be audible if they were sound waves (which they aren't).  Because of this, we can make them into sound waves by putting the signal through a speaker.  So we did!

Because the starting frequency of the gravitational wave is very low, it is difficult to hear.  The frequency is audible, but at that low of a frequency we tend to feel the sound vibration more than we hear it.  So unless you have a truly great subwoofer, you will probably only hear the end "whoop" of the signal.  In order to make the entire signal more audible, we shifted all of the frequencies up in the above sound up so you can hear the whole thing.  This is not unlike the false-color images made in astronomy for light that our eyes cannot see.

Now that you've heard the detected gravitational wave, you can see that when the tone of it becomes higher toward the end of the signal, the frequency in the spectrogram also goes up.


WHERE DID THE SIGNAL COME FROM?

Because the two LIGO detectors were the only detectors operating at the time of the event (Virgo in Italy is finishing their advanced detector upgrades and KAGRA in Japan is under construction with similar advanced instrumentation) it isn't easy to state precisely where the signal came from.  We can narrow it down to an area on the sky based on how long it took the gravitational wave to travel between the two LIGO detectors, and other factors like the strength of the signal in each detector (there is a slightly different response for each detector for different sky locations).  The most probable location is in the southern hemisphere around the constellations Volans and Carina:

The colored area on this map shows the most probable source of the detected gravitational wave where red is more likely than purple.  The location is shown against a map of the night sky centered on the Milky Way galaxy with constellations outlined.
[Credits: NASA Deep Star Maps (Visualization Credits, Ernie Wright (USRA): Lead Animator, Tom Bridgman (GST): Animator) by NASA/Goddard Space Flight Center Scientific Visualization Studio with constellation figures based on those developed for the IAU by Alan MacRobert of Sky and Telescope magazine (Roger Sinnott and Rick Fienberg), and the source location based on Gravoscope screen grabs (LIGO & Nick Risinger, skysurvey.org), all in galactic coordinates. Composition by University of Florida / S. Barke.]

 
WHAT MADE THIS GRAVITATIONAL WAVE?

Two different data analysis methods that look at the data in fundamentally different ways not only detected this event, but provided the same results for what the source of it was.  This gravitational wave was made by two stellar mass black holes (these are the remnants of extremely massive stars that have expended their fuel and collapsed under their own gravity).  As quoted above, their masses were about 29 and 36 times the mass of our Sun.  They orbited around each other for hundreds of thousands to millions of years before they come close enough together to start orbiting very quickly (much like an ice skater spins faster as they draw their arms into themselves).  LIGO was only sensitive to the very end of this process right before the two black holes merged into one black hole.  At the end, the stars had a relative velocity of about 1.8x10⁸ m/s, or 60% the speed of light (the universe's "speed limit").  Imagine that...  Two black holes that were each the size of cities but each about 30 times as massive as our Sun whirling around each other at more than half the speed of light!  The animation below shows what it may have looked like to see these black holes merge together.  Note that since they are black holes, no light come from them directly but they do bend the light that is coming from behind them in a process called gravitational lensing:

Based on how strong we know these gravitational waves were at their source as predicted by general relativity and how strong they were once they reached Earth, we estimate that this system is located about 1.3 billion light years (~410 Mpc) away.  That distance is about 10% of the way to the edge of the observable universe!  It also means that the gravitational waves we just detected have been traveling into the universe and toward us for 1.3 billion years.  When these gravitational wave were created the Earth was in the Proterozoic eon of Precambrian time, after when multicellular life developed but before animal life.

PRESS CONFERENCE RECORDING

Note:  Fast forward to 26:30.  It's just waiting before that. 

Next post: On the formation of stellar mass black hole and why this pair of them are interesting to astronomy...

Black Holes 101

Most of what I discuss on this blog has to do directly with gravitational waves.  This time I'd like to talk about one of their most talked about exotic sources: black holes.  Black holes are an exemplary source because they are highly concentrated mass.  Just add a touch of accelerated motion and gravitational waves are emitted in abundance (well, it's not quite that simple and "abundance" is a relative term, but you get the idea).  But what are the fundamental concepts that add up to the existence of black holes?  That's what we are focusing on now.


1.  Escape velocity

You've probably noticed that the harder you throw an ball straight up in the air, the higher it goes.  We also know that the farther away the ball gets from the Earth, the lower the gravitational attraction is between the ball and the Earth.  When you connect these two concepts, you can imagine that there is a speed at which you can throw the ball up and it will never come back down.  This is called the escape velocity:

We have discussed escape velocity before on this blog (specifically when discussing the conditions an object must have to be 'eaten' by a black hole).  In this equation, G is the gravitational constant, M is the mass of the 'thing' you are trying to escape, and r is the distance you are from the center of the 'thing'.  The bigger the mass of the 'thing', M, is, the faster the object must be thrown to escape it, v_e.

Going back to throwing a ball up in the air from the Earth's surface, you would need to throw that ball about 25,000 mph so that the ball would not come back to the Earth (good luck with that)!


2.  The speed of light is the universal 'speed limit'

Nothing can travel faster than the speed of light (in a vacuum), represented by c.  No matter, energy, or information about the Universe can travel faster than that.  That is pretty much the long and the short of this concept.

[Source: Knight Science Journalism at MIT blog]

This 'speed limit' comes from Einstein's special relativity and the effect of simultaneity.  Perhaps I will write a longer post about this in the future, but all that is important now is to recognize that if something needed to travel faster than the speed of light to communicate information to you, then you are never going to know about it.


3.  Light is affected by gravity

Light is both a particle and a wave.  As a particle, it has no mass.  Since gravity acts between two masses, it may be surprising that light can be affected by gravity at all!  But it does.  This effect is called gravitational lensing and I've written about this previously here. 


CONCLUSION:  How these concepts form a black hole

The simplest black hole is called a Schwarzschild black hole.  This is a black hole that has no electrical charge and is not rotating - it's just "there" meaning that there won't be anything to complicate our black hole situation.  For now, let us think of our black hole as having mass but no volume.  You can think of this as being the ultimate implosion.  Since this mass has no volume, there isn't any surface to it.  Eventually, as we get closer and closer to where the mass is centered, the escape velocity will become so large that the escape velocity will be greater than the speed of light.  And since light is indeed affected by gravity, that means that nothing will be able to escape the black hole.  We can even figure out what this distance is from the equation for escape velocity by setting v_e to the speed of light, c, and solving for r (the distance away from the mass where the escape velocity equals the speed of light):

This distance from a black hole where light will not be able to emerge from a black hole is also called the event horizon and this sphere around the black hole is what is being referred to when we talk about the size of the back hole.  For this simple Schwarzschild black hole, it is also known as the Schwarzschild radius.  You can also think of this radius as how small a mass would have to be to become a black hole.

So, how big would the Schwarzschild radius be for some things we are familiar with?  Well, for a black hole with the mass of our Sun it would be just about 3 km or about 1.9 miles.  For a black hole with the mass of the Earth it would be 8.87 mm or a little under 11/32" (0.349 in).

Gravity - The Love Story II: Starstruck!

So, where was I when I last posted...  Ahh... The great corny love story between two objects bound together by gravity.  I started that post asking what would happen to the Earth if the Sun were to suddenly become a black hole.  Many people think that the Earth would be sucked in because they assume that a black hole will suck everything into it like water going down a drain.  But, from careful examination of the universal law of gravitation and the story it tells, we see that isn't the case and the Earth will stay in the same orbit that is it now - no closer and no farther away.

But what about an object flying by a black hole (or any other massive object) instead of being in a nice stable orbit (like the Earth is in the previous example)?  This makes things a little more complicated, so I am going to let go of telling a love story.  That being said, there will be more equations here, but like the previous love story post the equations will only serve to help tell the story and we will not be using any numbers.


THE FATE OF A COSMIC WANDERER

Instead of looking at the universal gravitation law, we are going to look at how a passing object comes to be in orbit, or not, around another object (this governed by Kepler's laws of planetary motion).  To keep things simple, let's assume that the moving object has much, much less mass than the object it's passing (this is so that we can ignore the motion of the big object due to its gravitational attraction to the passing object).  Basically, picture something small whizzing through space (I'll call this the small object) that passes by a star or black hole (I'll call this the big object).  It is now safe to assume that any motion caused by gravity is going to be seen in the small object.


IT'S ALL ABOUT THE SPEED

The one factor that completely determines the fate of the small object is its speed.  If this speed is great enough, then the small object will be able to escape the big object, though its speed and direction will have changed.  The minimum speed at which the small object will not be captured into an orbit is called the escape velocity:

Here, we see that the escape velocity, v_e, changes as the square root of 1/distance (1/r) between the objects' centers.  That means that the closer the small object is to the big object, the more speed it must have in order not to get caught by it; the farther away, the less speed it needs to escape.  2GM is a constant value and never changes; G being the universal gravitational constant and M being the mass of our big object.


ORBITS AND ELLIPSES

Any speed less than the escape speed and the small object will be captured by the big object and will likely start orbiting the big object (or collide with it, we'll get to that later).  Let's say that we are traveling at a speed less than the escape velocity.  Kepler's laws of planetary motion (which are a consequence of gravitation) provide that the shape of the orbit is an ellipse (an oval shape).  Instead of having one center like a circle does, an ellipse has 2 each called a focus.  A classic way to draw an ellipse for yourself is to put two pins into a piece of paper, put a loop of string around the pins, place a pen in the loop and pull the loop taut.  The shape that you draw doing this is an ellipse:

[Image from: Wikipedia]

Here, each pin is a focus.  This is what having 2 "centers" means - if you were to draw a shape using this same method but using only one pin, then you would draw a circle (the pin being the true center).  When talking about an orbit of a very massive object and much smaller object (like we have in this example, or like the Earth orbiting the Sun), the more massive object will be located at a focus and there isn't anything at the other focus.

The speed of the object determines the shape of orbit:

Here v is the speed of the orbiting object (which is less than the escape velocity), μ is a constant (G times the mass of the big object), r is the distance from the objects' centers when the velocity is measured, and a is the semi-major axis of the ellipse (the distance between the midpoint of the foci and the farthest point of the ellipse). 

[Image from: Wikipedia]

STARSTRUCK!

Under what conditions does the small object collide with the big object?  So far it sounds like the small object is either going to escape the gravitational pull of the big object or start orbiting it.  Can a black hole (assuming it's our big object) ever "swallow" anything?  Yes, indeed, but only under certain conditions...

To determine the conditions for an object to be swallowed by a black hole or collide with a star, we need to realize that neither of these objects is a nice point as we have been treating them (well, the singularity inside the black hole is a nice point, but more on that below).  Instead, objects occupy a volume and the points we were considering were really the center of mass of the object (approximately the actual center for a spherical object).  So, the small object will collide with the big object if the radius of the big object is more than the distance of closest approach of the small object's orbit.  This distance is called periapsis and is the distance along the red line (the semi-major axis) between the ellipse (orbit) and the focus (the big object) in the previous figure.  If a star has a radius of this or more, then the small object will slam into it.

NOTE:  This scenario for collision (and the one for merger with a black hole below) assumes that the objects only interact through gravity.  That means that there is no consideration here for other forces like the interactions of the objects' magnetic fields (if they have them) or resistance from the matter and radiation that stars tend to spew out.


HUNGRY, HUNGRY, BLACK HOLES

But what about the specific case of a black hole?  I mention that there is a point-like singularity in the black hole where all the mass is located.  How do we determine the shape of the whole black hole?  First, consider why a black hole is called "black"; because the gravity inside of it is so strong that the speed of light is less than the escape velocity (now you can think of our small object as a photon of light).  Since nothing can travel faster than the speed of light, nothing can escape a black hole.  So we define the edges of the black hole to be the radius at which the escape velocity equals the speed of light.  This radius is called the event horizon.  Therefore, an object (even a photon) will merge with a black hole when the distance of closest approach of its orbit is equal to or less than the event horizon.

Now that's what I call "starstruck" lovers!  Get it?  The small object strikes the big object which could be a star...  Okay, I know it's lame, but that's why I'm a physicist and not a comedian (though I do try!).

---

 

♥  Speaking of love, happy anniversary to my husband, Derek, who is always nice enough to proofread these posts.  We've been together for 16 years, married for 9 and looking forward to many more!  ♥

Gravity - The Love Story I: Black Holes Are Not 'Universal' Drains

This semester I am teaching a conceptual physics class at LSU that uses minimal mathematics to understand how the Universe works.  Yesterday, we covered the chapter on gravity and my closing question to my students was, "What would happen to the Earth's orbit if the Sun were to become a black hole instantly?"  Assume that it simply changes in size from what it is now to how big a black hole with the same mass would be and the center of mass never changes.

I'm not going to make you wait...  Nothing would happen to the Earth's orbit!

This is one of the most dramatic examples of simply using an equation to tell a story that I have come across.  I suspect that much of the drama comes from the misconception that black holes WILL consume EVERYTHING, turning most people's mental picture of a black hole into a universal drain.

(I know the following analogy is a bit corny, but it makes the point that equations can tell stories and aren't just recipes to combine numbers into new numbers...)


EQUATIONS TELL A STORY

In order to resolve this misconception, consider Newton's law of universal gravitation:

  

Now, don't worry overly that this is an equation because we will be making no calculations.  Instead, we are going to use it as a script for a play.  This play just so happens to be a love story...  ♥


THE CAST OF CHARACTERS

On the left side of "=" we don't have a character, but the ending of our story: F.  (This is the gravitational force that will be felt between two masses.)  We can also think of F as the attraction between our characters.  Therefore, the larger the attraction F, the better the 'Happily ever after...' ending.

The story is told by our characters on the right side of "=": G, m₁, m₂, and r:

• G is a VERY small constant that is fundamental to the Universe.  That is, there is no way to derive its value from any theory, we simply determined this value from measurements.  Since G doesn't change, it is more of a background prop than a character; we don't need to worry about it since the moral of our story will be the same with or without it.
• Next we have our two lovers: masses m₁ and m₂.  I call them lovers because they are attracted to each other (literally since gravity tends to pull mass together).  
• Finally, we have our villain, r, who keeps our lovers apart.  (This is the distance between each of our lovers' center of mass.)  

That is the complete cast of characters in this story!  There are no extras milling around in the background.


THE PLOT

When you multiply G, m₁, and m₂ together and then divide by r² (which is equivalent to r*r), you are able to determine the ending to our story which is the attraction (F) between our lovers.  Now we are able to establish some plot points:

• The more massive either of our lovers (m₁ or m₂) are, the more they will be attracted to each other.
• The farther apart (r) they are, the less they will be attracted to each other; the bigger the number you divide by, the smaller your result.  (The square on r only serves to make the reduction in attraction between our lovers less even faster.  For example, if you double the distance between the lovers, you quarter their attraction.)

THE SUBPLOT

Now let's take a look at some of the more subtle plot points, specifically the properties that determine the attraction of our lovers (m₁ and m₂):

• No unrequited love:  m₁ and m₂ are always equally attracted to each other.  It doesn't matter if one is more massive than the other.  
• Love is blind:  There is nothing in our script which describes the size or shape of our lovers.  Assuming m₁ and m₂ stay the same distance apart and their masses don't change, they will always be equally attracted to each other.  m₁ will love m₂ the same regardless of whether its mass is made up of dense muscle or voluminous blubber. 

"ACTION!"

Now that we have the script to our play, let's see how the ending turns out when we cast the Sun as m₁ and the Earth as m₂.  The scene opens the with Earth orbiting the Sun a fixed distance r away (this is called an astronomical unit, AU, and it is about 93 million miles).  We sit and watch the Sun and the Earth be attracted to each other, but the villain of distance keeps them apart.  In an attempt to overcome our villain, the Sun decides to implode on itself, sucking all of its mass into a ball less than about 3.72 miles across.  Now it is a black hole but, according to our script, the Earth felt no change since its love it blind!  The mass of the Sun didn't change and its center is still in the same place.  Drat, the Sun didn't succeed in increasing its attraction with the Earth!

~ FIN ~

♥  Stay tuned for the next installment of "Gravity - The Love Story"!  We will find out what properties our lovers need to have to come together (that is, what properties a mass needs to have to actually get "eaten" by a black hole).  ♥